Abstract
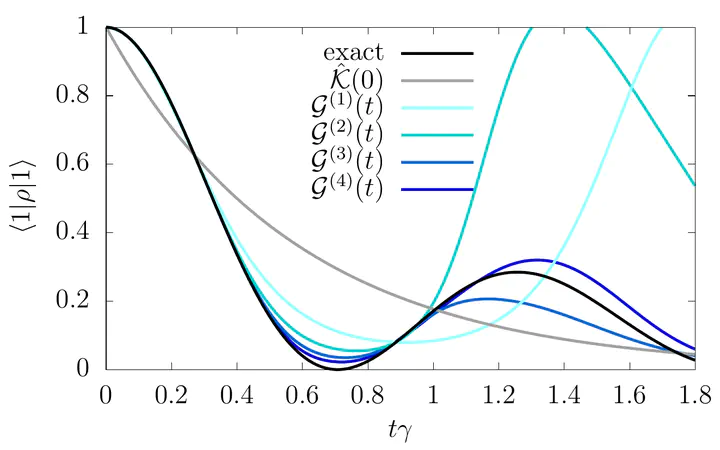
In this thesis we consider the dynamics of generic open quantum systems described using quantum master equations (QMEs). Motivated by the puzzling fact that there are two exact QMEs, the time-nonlocal (Nakajima-Zwanzig) and the time-local (time-convolutionless) QME, our focus is finding the general connection between these two canonical approaches. The result takes the form of an elegant functional fixed-point relation between the time-local generator $\mathcal{G}$ and the time-nonlocal memory kernel $\mathcal{K}$, $\mathcal{G}=\hat{\mathcal{K}}[\mathcal{G}]$. This leads to several new insights into important topics in open system dynamics, including the construction of non-perturbative Markov approximations, their relation to initial slip corrections, and a memory expansion used in studies of driven quantum dynamics and transport. Furthermore, it naturally suggests a novel construction of time-local descriptions from iterations of the fixed-point functional, which we explore in detail for the Jaynes-Cummings model describing atomic decay in a radiation field and the resonant level model describing non-interacting transport to an electron reservoir.
We further leverage this relation to derive the general connection between time-local and time-nonlocal perturbation expansions, a long-standing problem. This allows the technically more advanced time-nonlocal approximation strategies to be translated into a corresponding time-local picture, which is advantageous from the quantum information vantage point. We exemplify this using the Anderson model of an interacting quantum dot coupled to voltage-biased electron reservoirs to show how the well-known diagrammatic expansion of the time-nonlocal memory kernel can be translated into its time-local form term-by-term. Additionally, we apply this technique to investigate a powerful renormalized series, which reveals limitations of the time-local approach.
Finally, based on this series we introduce a time-nonlocal renormalization group to address the interesting low-temperature dynamics of Anderson-like models. This method works by lowering the environment temperature and calculating the higher order coupling effects this generates. One of its key features is that a single renormalization group trajectory contains the full temperature dependence of dynamical and transport quantities. The method can be formulated in real-time, which brings several advantages, in particular for analyzing transient dynamics. Our numerical results are benchmarked against several other advanced methods, such as the functional renormalization group, the density-matrix renormalization group, and the quantum Monte Carlo method.