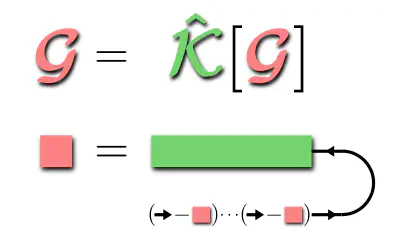
Abstract
Two widely used but distinct approaches to the dynamics of open quantum systems are the Nakajima-Zwanzig and time-convolutionless quantum master equation, respectively. Although both describe identical quantum evolutions with strong memory effects, the first uses a time-nonlocal memory kernel $\mathcal{K}$, whereas the second achieves the same using a time-local generator $\mathcal G$. Here we show that the two are connected by a simple yet general fixed-point relation: $\mathcal{G} = \hat{\mathcal{K}}[\mathcal{G}]$. This allows one to extract nontrivial relations between the two completely different ways of computing the time-evolution and combine their strengths. We first discuss the stationary generator, which enables a Markov approximation that is both nonperturbative and completely positive for a large class of evolutions. We show that this generator is not equal to the low-frequency limit of the memory kernel, but additionally samples it at nonzero characteristic frequencies. This clarifies the subtle roles of frequency dependence and semigroup factorization in existing Markov approximation strategies. Second, we prove that the fixed-point equation sums up the time-domain gradient / Moyal expansion for the time-nonlocal quantum master equation, providing nonperturbative insight into the generation of memory effects. Finally, we show that the fixed-point relation enables a direct iterative numerical computation of both the stationary and the transient generator from a given memory kernel. For the transient generator this produces non-semigroup approximations which are constrained to be both initially and asymptotically accurate at each iteration step.
→ See press releases by RWTH Aachen, FZ Jülich and JARA