General connection between time-local and time-nonlocal perturbation expansions

Abstract

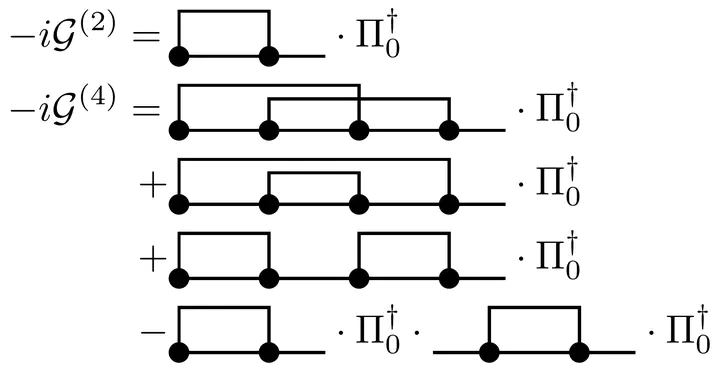
There exist two canonical approaches to describe open quantum systems by a time-evolution equation: the Nakajima-Zwanzig quantum master equation, featuring a time-nonlocal memory kernel $\mathcal{K}$, and the time-convolutionless equation with a time-local generator $\mathcal{G}$. These key quantities have recently been shown to be connected by an exact fixed-point relation [Phys. Rev. X 11, 021041 (2021)]. Here we show that this implies a recursive relation between their perturbative expansions, allowing a series for the kernel $\mathcal{K}$ to be translated directly into a corresponding series for the more complicated generator $\mathcal{G}$. This leads to an elegant way of computing the generator using well-developed, standard memory-kernel techniques for strongly interacting open systems. Moreover, it allows for an unbiased comparison of time-local and time-nonlocal approaches independent of the particular technique chosen to calculate expansions of $\mathcal{K}$ and $\mathcal{G}$ (Nakajima-Zwanzig projections, real-time diagrams, etc.). We illustrate this for leading and next-to-leading order calculations of $\mathcal{K}$ and $\mathcal{G}$ for the single impurity Anderson model using both the bare expansion in the system-environment coupling and a more advanced renormalized series. We compare the different expansions obtained, quantify the legitimacy of the generated dynamics (complete positivity) and benchmark with the exact result in the non-interacting limit.